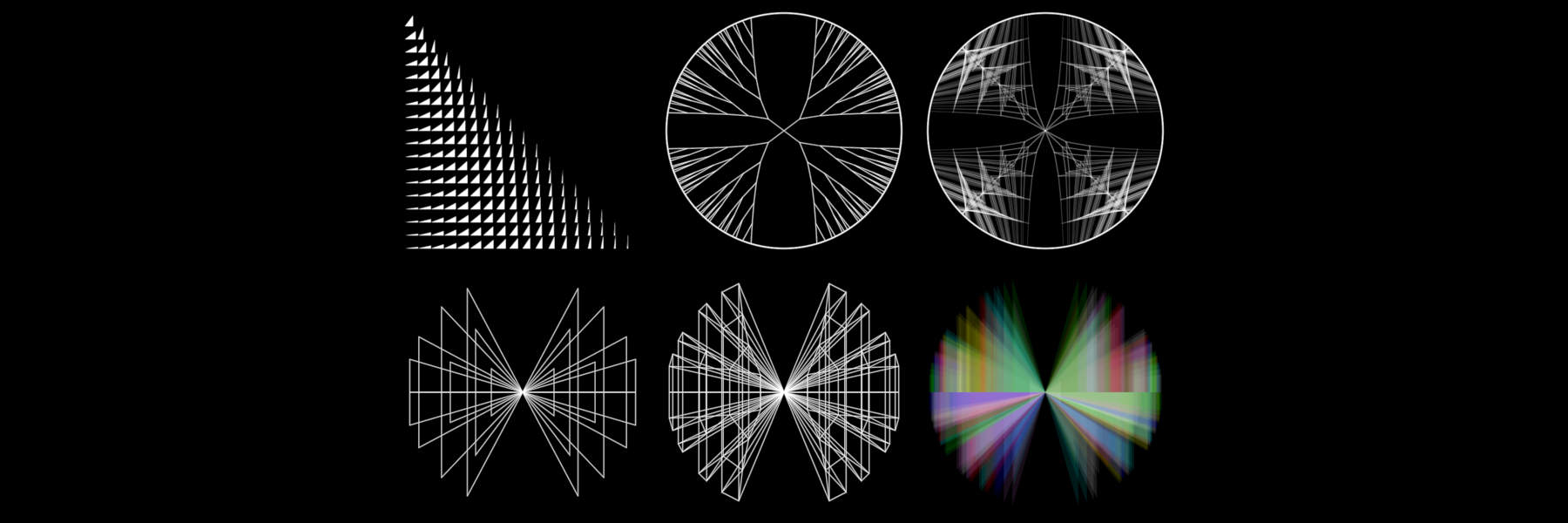
The stereographic projection of the Stern–Brocot tree
Classical enumeration
What looks like triangles doing yoga is the classical enumeration of Pythagorean triples.
With each row the number of columns increases by one. Each cell shows a right triangle with side lengths that are natural numbers. If we number the rows , the columns , then the legs and the hypotenuse are defined by
which guarantees, that
The triplet is called Pythagorean triple and this method produces every possible Pythagorean triple [X].
Dividing by on both sides
makes it clear, that all Pythagorean triples can be mapped onto rational points on the circle. Conversely, it can also be shown, that all all rational points on the circle can be mapped to primitive triples — those where and are coprime. So, primitive Pythagorean triples and rationals points on the circle are isomorphic.
The following table shows again the triangles with their classical coordinates and the actual triples at the bottom. Triangles of non-primitive triples are hatched.
Although it is known that the coordinates of non-primitive triangles are those where and are coprime and not both odd, the remaining table does not give any hierarchical order of the triangles by, for example, acuteness.
Such a hierarchical construction of primitive triples was discovered in 1963 by the Dutch mathematician Barning, and later independently by others.
Barning–Hall tree
The Barning–Hall tree is a ternary tree.
We encode the triples as 3-vectors and define the root of the tree as . The tree is then spanned by recursive left multiplication of the one of the three matrices
Using this technique, we can now enumerate triples by paths in the tree. For example, the triple is obtained by first applying and then to the root. A few more examples:
To get a visual idea of the tree, the following diagram maps the nodes to their rational counterparts on circle quadrants whose radii increase with each level. The edges cross each other and are colored , , and to make the structure clearer.
The trisecting property of the Barning–Hall tree shines out. Paths ending in have smaller turn angles — or triangles that are more acute — than paths ending in . And paths ending in have smaller turn angles than paths ending in .
Furthermore, one could conjecture
That is, the upper boundary of the red sector converges to the lower boundary of the green sector, and the upper boundary of the green sector converges to the lower boundary of the blue sector.
However, the tree does not cover the whole circle quadrant because the it does not contain permutations of triples. For example, is part of the tree, but not . To describe all points, another copy of the tree with the root would be needed.
Also, the braided nature of the tree does not allow for a hierarchical ordering of the paths by turn angle.
Such an order is provided by a simpler enumeration covering all rational points on the full circle, the stereographic projection of the Stern–Brocot tree, which will be the subject of the rest of this text.
Stereographic projection of the Stern–Brocot tree
The Stern–Brocot tree is a binary tree enumerating all rational numbers by value and complexity and following diagram shows its stereographic projection through the pole , given by
Like in the Barning–Hall case above, tree nodes are drawn on circles with radii increasing by each level. The turn angle is indicated in green.
It's immediately clear, that the order of projected numbers is in some way preserved because the stereographic projection is part-wise monotonic.
As far as I am aware, this construction has not been thoroughly studied and I believe there is still much to be discovered. There are several properties that right out catch the eye, but before describing the tree further, I show how it can be utilized to connect turn angles to points on the circle.
Turn angles
To compute turn angles of rational points on a circle straight out as Stern–Brocot sequences, I think it's simplest to combine the following two key ideas.
First, we view the points as complex numbers , and note the additivity of turn angles under complex multiplication.
If we name the turn angle , the following equalities hold
Second, to compare turn angles, we consider and embedded in three-dimensional Euclidean space and exploit of the right-handedness of the cross product.
If we place the projection plane at , the coordinates are
Now we can define a segment . A point is in the segment if the z-component of the cross product is positive. Written out in terms of coordinates this is
The algorithm is now similar to Euclid's algorithm. First, we look how often fits in the full circle by finding s.t. . We then know the first term of the continued fraction of the inverse turn angle
We then divide by to get a circle point having the left over turn angle. We then look how often fits into by finding s.t. . We now got the second term
and recur by looking how often fits into .
An algorithm for stepwise output of Stern-Brocot sequences might look like this
turn(p): return inv(turn'(p,p,p,R))turn'(p, a, q, dir): a' ← a·p if q ∊ segment(a,a'): turn'(q/a, (1, 0), p, flip(dir)) else: output dir turn'(p, a', q, dir)
Since there are no rational points on the circle with rational turn angles — except the poles — this recursion will never end, but with each bit, we get the next best rational approximation of the angle.
By combining the stereographic projection with the turn, we are now able to compute best approximations of trigonometric functions.
Trigonometric functions
As is so often the case in circular geometry, a distinction must be made according to quadrant.
I will only describe the first, the other three quadrants can be treated in a similar way.
Rational points in the first quadrant are stereographically mapped onto points on the number line greater than 1, i.e. sequences starting with . Furthermore, the projection is monotonic as larger values on the number line map to circle points with larger turn angles.
To find the circle point corresponding to a turn angle , we start with the stereographic projection of and compute its turn angle with the algorithm described above. If the computed turn angle is larger than , we append an and do the same with the projection of . If the computed angle is smaller than , we append an and recur.
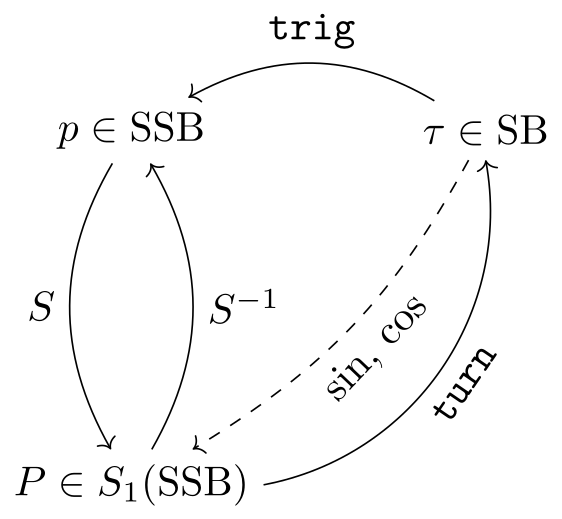
Assuming that the conjecture that stereographically projected Stern–Brocot sequences order circle points hierarchically like fractions on the number line is somehow true, we could say that we can now compute best approximations of circle points for turn angles.
This means that we also can compute best approximations of trigonometric functions, because the x-coordinate of the circle point is the cosine of the turn angle, the y-coordinate the sine.
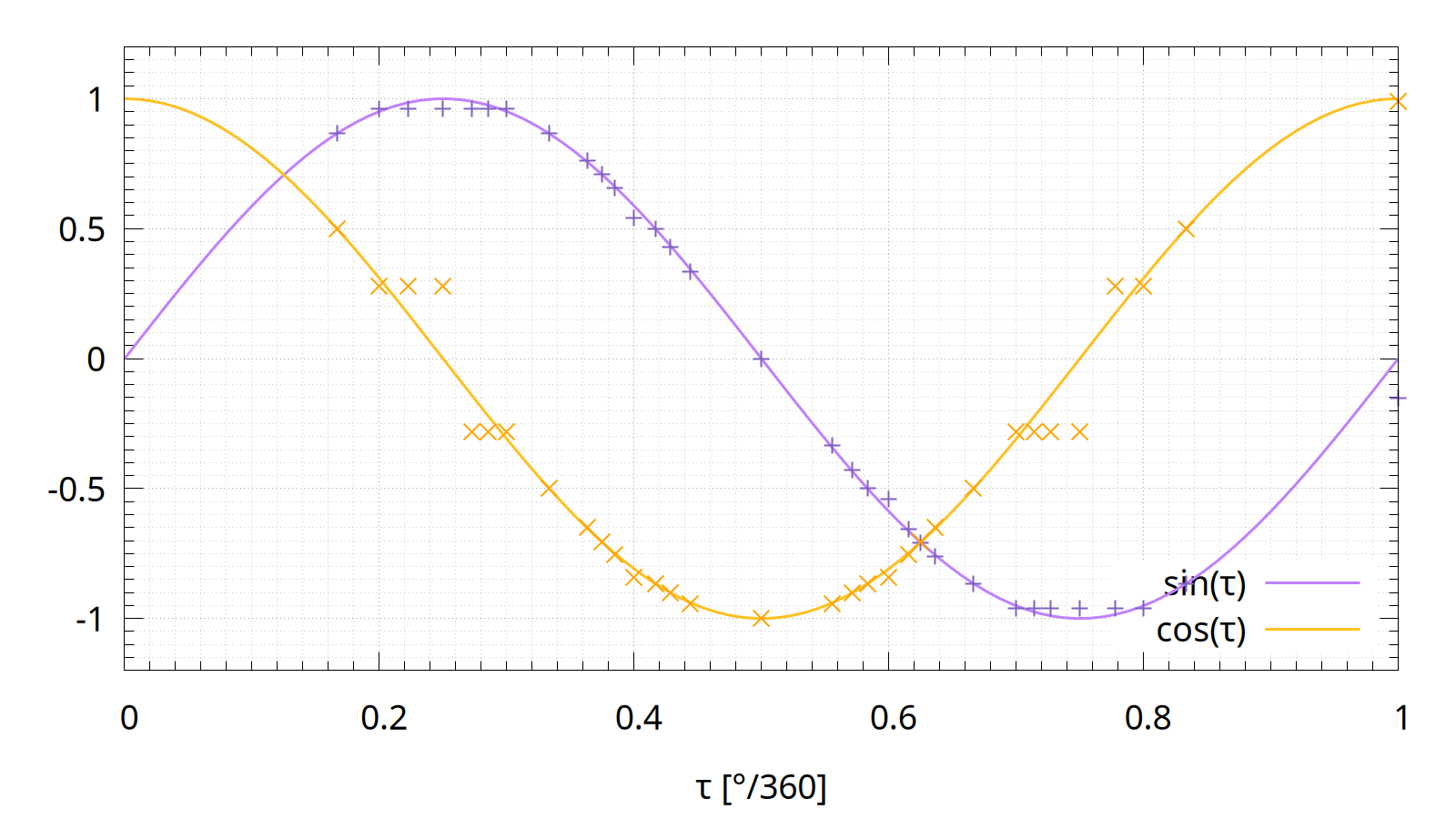
Since my current implementation of Stern–Brocot arithmetic is very slow — it does not even use tail call optimization — the computations quickly exceed the stack size.
For now, the stereographic projections of turn angles are computed up to 7bit.
| τ (SSB) | τ (IEEE754) | p (SSB) | cos (IEEE754) | cos (CF) | sin (IEEE754) | sin (CF) |
|---|---|---|---|---|---|---|
| ○○○○○ | 0.1666666666666667 | ●●●○●● | 0.4979253112033195 | [0,2,120] | 0.867219917012448 | [0,1,6,1,1,7,2] |
| ○○○○ | 0.2 | ●●●●●● | 0.28 | [0,3,1,1,3] | 0.96 | [0,1,24] |
| ○○○○● | 0.2222222222222222 | ●●●●●● | 0.28 | [0,3,1,1,3] | 0.96 | [0,1,24] |
| ○○○ | 0.25 | ●●●●●● | 0.28 | [0,3,1,1,3] | 0.96 | [0,1,24] |
| ○○○●○ | 0.2727272727272727 | -●●●●●● | -0.28 | -[0,3,1,1,3] | 0.96 | [0,1,24] |
| ○○○● | 0.2857142857142857 | -●●●●●● | -0.28 | -[0,3,1,1,3] | 0.96 | [0,1,24] |
| ○○○●● | 0.3 | -●●●●●● | -0.28 | -[0,3,1,1,3] | 0.96 | [0,1,24] |
| ○○ | 0.3333333333333333 | -●●●○●● | -0.4979253112033195 | -[0,2,120] | 0.867219917012448 | [0,1,6,1,1,7,2] |
| ○○●○○ | 0.3636363636363636 | -●●○●●○ | -0.648780487804878 | -[0,1,1,1,5,1,1,5] | 0.7609756097560976 | [0,1,3,5,2,4] |
| ○○●○ | 0.375 | -●●○○●● | -0.7041420118343195 | -[0,1,2,2,1,1,1,2,2] | 0.7100591715976331 | [0,1,2,2,4,2,2] |
| ○○●○● | 0.3846153846153846 | -●●○○○○ | -0.7534246575342466 | -[0,1,3,18] | 0.6575342465753425 | [0,1,1,1,11,2] |
| ○○● | 0.4 | -●○●●●● | -0.8407643312101911 | -[0,1,5,3,1,1,3] | 0.5414012738853503 | [0,1,1,5,1,1,6] |
| ○○●●○ | 0.4166666666666667 | -●○●●○● | -0.867219917012448 | -[0,1,6,1,1,7,2] | 0.4979253112033195 | [0,2,120] |
| ○○●● | 0.4285714285714286 | -●○●○○● | -0.902970297029703 | -[0,1,9,3,3,1,3] | 0.4297029702970297 | [0,2,3,17,1,3] |
| ○○●●● | 0.4444444444444444 | -●○○●●○ | -0.9422632794457275 | -[0,1,16,3,8] | 0.3348729792147806 | [0,2,1,71,2] |
| ○ | 0.5 | -1 | -1.0 | -[1] | 0.0 | [0] |
| ○●○○○ | 0.5555555555555556 | -○●●○○● | -0.9422632794457275 | -[0,1,16,3,8] | -0.3348729792147806 | -[0,2,1,71,2] |
| ○●○○ | 0.5714285714285714 | -○●○●●○ | -0.902970297029703 | -[0,1,9,3,3,1,3] | -0.4297029702970297 | -[0,2,3,17,1,3] |
| ○●○○● | 0.5833333333333333 | -○●○○●○ | -0.867219917012448 | -[0,1,6,1,1,7,2] | -0.4979253112033195 | -[0,2,120] |
| ○●○ | 0.6 | -○●○○○○ | -0.8407643312101911 | -[0,1,5,3,1,1,3] | -0.5414012738853503 | -[0,1,1,5,1,1,6] |
| ○●○●○ | 0.6153846153846154 | -○○●●●● | -0.7534246575342466 | -[0,1,3,18] | -0.6575342465753425 | -[0,1,1,1,11,2] |
| ○●○● | 0.625 | -○○●●○○ | -0.7041420118343195 | -[0,1,2,2,1,1,1,2,2] | -0.7100591715976331 | -[0,1,2,2,4,2,2] |
| ○●○●● | 0.6363636363636364 | -○○●○○● | -0.648780487804878 | -[0,1,1,1,5,1,1,5] | -0.7609756097560976 | -[0,1,3,5,2,4] |
| ○● | 0.6666666666666667 | -○○○●○○ | -0.4979253112033195 | -[0,2,120] | -0.867219917012448 | -[0,1,6,1,1,7,2] |
| ○●●○○ | 0.7 | -○○○○○○ | -0.28 | -[0,3,1,1,3] | -0.96 | -[0,1,24] |
| ○●●○ | 0.7142857142857143 | -○○○○○○ | -0.28 | -[0,3,1,1,3] | -0.96 | -[0,1,24] |
| ○●●○● | 0.7272727272727273 | -○○○○○○ | -0.28 | -[0,3,1,1,3] | -0.96 | -[0,1,24] |
| ○●● | 0.75 | -○○○○○○ | -0.28 | -[0,3,1,1,3] | -0.96 | -[0,1,24] |
| ○●●●○ | 0.7777777777777778 | ○○○○○○ | 0.28 | [0,3,1,1,3] | -0.96 | -[0,1,24] |
| ○●●● | 0.8 | ○○○○○○ | 0.28 | [0,3,1,1,3] | -0.96 | -[0,1,24] |
| ○●●●● | 0.8333333333333333 | ○○○●○○ | 0.4979253112033195 | [0,2,120] | -0.867219917012448 | -[0,1,6,1,1,7,2] |
| 1 | 1.0 | ○●●●●● | 0.9882352941176471 | [0,1,84] | -0.1529411764705882 | -[0,6,1,1,6] |
A fast implementation as well as an FPGA design for Stern–Brocot arithmetic are among my current hobby projects.
Appendix
The diagram below illustrates how Pythagorean triples can be indexed using the stereographic projection of the Stern–Brocot tree. Tree nodes can be selected by clicking on them or using the slider controls on the right.
References
[X] Book X, Proposition 29, Euclid's Elements, Clark University
[B] Barning, F. J. M. (1963). Over pythagorese en bijna-pythagorese driehoeken en een generatieproces met behulp van unimodulaire matrices. Stichting Mathematisch Centrum. Zuivere Wiskunde. Stichting Mathematisch Centrum.